スーパーでずっと売れ残っていた（おそらくバレンタインデーあたりから？）チョコの家を買ってみた。売価525円の半額＆11％引きのコンボで234円、板チョコ３枚分の価格で、板チョコ換算６枚分のチョコを買ったことになる。チョコ好きにはお買い得である。
うちは板チョコをばりばり食ってしまうヒトが多数なので、組み立て後、あっという間に無くなってしまった。
ちなみに沖縄名物紅いもタルト（ポルシェ謹製）も半額で購入。即消費である。
» 生活のブログ記事
上から見たもの
近畿地方の梅雨入りの平年値が６／７なので10日も早い。
と思って調べてみたら２年前は５／２２、５年前も５／２８。
追記 20130530
梅雨前線も明確に出来ていないのに、なぜ今年は梅雨入りが早々に宣言されたのか、疑問に思っていた。以下読売新聞社の記事より抜粋。
『毎年６月頃になると、…偏西風が押し上げられ、南から暖かく湿った空気が流れ込み、…大気の状態が不安定になり、雨雲が発生しやすくなる。』
『今シーズンは、海水温の上昇が例年より早く、偏西風が北に押し上げられる時期も早まった。』
ということらしい。そして梅雨明けに関しては平年並という予測らしく、今年は長梅雨となるそうだ。
外出時のデータ通信用に、docomo回線を利用するIIJ-mioをサービス開始より契約している。
これはLTE回線が利用できる3枚のSIMを月額2940円で１0Gまで、それ以降も200kbpsで利用できるというもの。
仕事中はメールすら見る余裕はないし、通勤も車なのでネットは使わない。外出も滅多にしない。なので相棒さんと2人合わせても一月400M程度しか使用しておらず、１0Gを使い切ったことは一度も無い。もったいないと思っているが、サービス自体はたいへん使い勝手が良いと思っている。
さて今までモバイルルーターにこのSIMを入れ、iPad-miniで利用したり、SIMが直接入るdocomoのタブレットを利用したりしていたわけだが、さすがに携帯を含め3台も持ち運ぶのが億劫に思えてきた。
かといってdocomoのパケホーダイなどバカ高くて加入できるものではない（中学生に聞いてみると一人あたり5000円程度の通信費は今や常識！らしいのだが）。来年には上娘も高校入学となり、一家の通信費を極力抑える準備に入ることにした。
で、IIJ-mioのSIMを、ネット端末で使うだけでなく電話も使う方法を探ってみた。
まずはモバイルルーターに代わり、テザリングのできるケータイを用意する。うちの場合は、2年前に契約して（すでに解約した）イーモバイルのS41HWがある。こいつはSIMフリーであり、テザリングもできる神機である。ちなみにdocomoのスマートフォンも基本的にはSIMフリーなのだが、テザリング時にSPモードに接続する仕様となっており、IIJ-mioなどのMVNOのSIMはテザリングできないようになっている（悪さをしない限り）。
このS41HWでテザリングすればiPad-miniなどのタブレット類を用いることができる。もちろん、この端末だけでもネット検索やメール程度ならできる。
残りは通話である。
ここでIPフォンで出番だ。050プラスが有名だが、今回はフュージョン・コミュニケーションズのFUSION IP-Phone SMARTを契約した。050プラスに比べ、固定電話への通話料は高いが、月額使用料0円が決め手である。使わなければ無料。通話料も30秒8.4円なので、私のようにたまの外出時に使うだけなら実に格安である。ただ問題もある。110など緊急通信が利用できない。これでは電話としては不安が残る。当面docomoなどのキャリアも残さないといけないか…。
まぁしばらく通話品質を調べるために使ってみることにする。
0505で始まる電話がかかってきたら、それは私かもしれません。
久々に募金を促すメッセージが出た。
まぁ何やかんやと世話になっているサービスなので、これから毎月少しずつ募金することにした。
液晶タブレットモニタ付きのパソコンだったが、本体のHDDがダメっぽく、世代交代することに。
以前使っていたCube型のwindowsXP機＋17インチのwacom液晶タブレットモニタの組み合わせ。
SXGA（1280×1024）なので、デスクトップが広い。
学割で買っていたOneNote2010もインストールした。
写真右端はandroid端末。
さて、身近なものをいろいろと拡大しては写真に撮ることを楽しめるデジタル顕微鏡であるが、透過光撮影もしたくなるというものだ。
ということでさっそく改造(笑)だ！
必要なもの
１.光源
２.透過してきた光を通す穴
今回は、１００円ショップのブツを中心に工作してみた。
まず１.の光源だが、これはLEDのクリップライトを改造。
写真の青色の部分をねじり取り、電池や回路･LEDが仕込まれている白色部分だけにする。
LEDが明るすぎるので、LEDが収納されている部分を開け、LEDの向きを逆にして、白いプラ越しに光を出すようにした。
２．の穴あけは力わざだ。
まず、顕微鏡のステージの部分を外す。
せまい部分のねじを緩める際には１００円ショップで買っておいたラチェットレンチが役に立った。
写真の左はステージの下部分、中央がステージの上部分。
今回の工作では、上部分の中央に穴を開ける。
使用する工具…はんだごて。
まったくの目的外使用であるが、それなりに厚みのあるプラに穴を開けるのには、実はかなり有効。
穴を開けたい場所に熱したコテを刺していく。
このとき、身体に悪そうなガスが出るので、換気扇はフル回転で。
次にニッパであけた穴の間を切り取っていく。
開いた→
カッターで出っぱった部分を削り取り、
やすりで形を整える。
光源部とステージを裏側でガムテープ留めする。
見てくれ的にも強度的にも、外したステージの下部分をつけたいところだが、まぁ実用十分なので良しとする。
しかし、このままではステージに穴が開いたまま。
・従来の反射光でステージ上の物体を観察
・穴の下からの透過光でプレパラートを観察
この両方を実現するために、ステージの上に、片側に穴の開いた板を置き、元からあったクリップで半固定した。
クリップで固定しているだけなので、穴の開いた部分と穴の無い部分を必要に応じて選択できる。
穴の開いた板は、これまた１００円ショップで買った「ソフトミニまな板」の指を入れる部分を切り取った。
さらに梨地の半透明プラを貼り付け、直進性の強いLEDの光が多少、拡散するようにしている。
【 完成 】
← 透過光用
クリップライトのスイッチを入れると穴の下から光が差す。
→ 反射光用
ソフトまな板を左にずらすと穴がかくれる。
で、普通の顕微鏡みたいに透過光での観察も出来るようになったわけだが…、
← 食塩の結晶〔透過光〕
うーん、残念ながら透過光で観察するにはレンズの倍率が足りなかったようだ。
まぁ工作としては面白かったから良しとしよう。
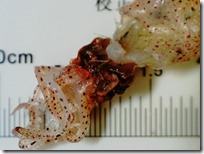
→ シラスに入っていた
チリメンモンスター
（イカの子ども）
〔反射光〕
講義形式の授業の時、自分の撮った写真やビデオ映像を見せたい時がある。
しかしパソコンやプロジェクター、マグネット式のスクリーンなど一式を持って移動し、セッティング、片付けとなると、けっこう大変なのである。
その一コマだけ授業をすればよいのなら、手間は惜しまないが、実際には次の授業の準備もあるし、生徒対応などもある。
どうしてもよほどの効果があるもの以外は、資料集の写真やお話で済ませてしまうことになる。
しかし。見せたい写真は山ほど有るのに、見せずに終わってしまうのは、毎回残念に思っていた事であり、写真を趣味にする私にとっては忸怩たる思いである。
そこで、意を決して持ち運びができるサイズのプロジェクターを買った。
そんなに大きく映すわけでも、屋外で映すわけでもないので、それなりの明るさでよい。
（と言っても昨年買ったプロジェクター付きデジカメは、明るさが10ルーメンでさすがに力不足であった）
買ったのはアドトロンテクノロジーのQUMI-Q2、後発のDell-M110と迷ったが、MS-Officeのデータがそのまま映せるのがポイントとなった。
写真の上の部分がプロジェクター。下は‥‥巨大モバイルバッテリである。今回プロジェクター購入と同時に注文した。
もちろんプロジェクターにはACアダプタが付属しているが、持ち運びを考え、なるだけコードレス化を目指したのだ。
（まぁバッテリとの間はコードデスが）
サイズは162x102x32mm、かなり小さい。子どもの弁当箱くらいか。
左の写真で腕時計と比較して欲しい。サイズがおわかりだろうか。
この小ささで明るさは300ルーメン。
教室内で1mくらいの距離からなら十分な明るさである。
>>>>と思ったのだが、先日実際に使ってみたところ、明るさは不十分であることが判明。冬場は室内まで光が入り込むためだ。
バッテリは23000mAhの巨大サイズ。19V3A出力のできるものを探してこれに行き着いた。
実験してみると、フル充電から、プロジェクターをつけっぱなし（3秒おきにスライドショー）にして、2時間30分ほど持った。
まぁ一日使う分には十分だろう。つけっぱなしにするような使用状況ならACアダプタをつなぐだろうし。
ちなみに外観が同じで出力が２Aのものが多く出回っているので、購入する際には注意が必要だ。
こちらは小型USBメモリ。今回買ったプロジェクターはMicroSDカードとUSBメモリに対応している。
USBならPCとのやりとりも間違いなくできる。このUSBメモリに必要な画像や映像を入れておき、プロジェクターに指せば、
上のセットを持ち運ぶだけでどこでも映写することができるわけだ。
ちなみにPPシートを使って折りたたみ式のスクリーンも作った。持ち運びを考えて写真のように4つに折りたためるようにしている。
PPシートは表面が梨地っぽくなっているので、光を適度に反射する。そしてしなやかなので、カッターで軽く切れ込みを入れると折れ曲がるけど切れないという絶妙な素材だ。
裏面には黒板に貼れるようにマグネットをつけている。収納時はこのマグネットどうしがくっついて勝手に展開しないので便利である。
２つの数字の最大公約数と最小公倍数‥‥これをプログラム的にどうするのか考えて見た。
まず最大公約数を求めて、二つの数を最大公約数で割った商をかけ合わせれば最小公倍数になる。
そのためには、共通して割れる素数を見つけ、どんどん割っていけばよい。割れなければ次の素数へ、これを繰り返す作業だ。
二つの整数を a,bとする。
最大公約数になる数字をcとする。
二つの数字を共通して割れる数字(約数)をiとする。
表の右端は例として、a=48 b=36 の場合を表示している。[]内の数字はループの回数。
| コード | 説明 | 具体例 | |
| c=1 | 最大公約数の初期値は1 | ||
| i=2 | 約数の初期値は2 | ||
| Do | Loop まで繰り返す | ||
| If (((a mod i)=0) and ((b mod i)=0)) then | もし aもbもiで割り切れるなら 以下の処理をする |
[1]OK [2]OK [3]NG [4]OK |
|
| a=a/i | aをiで割る | [1] a=24 [2] a=12 [4] a=4 |
|
| b=b/i | bをiで割る | [1] b=18 [2] b=9 [4] b=3 |
|
| c=c*i | 最大公約数になるcをi倍する | [1] c=2 [2] c=4 [4] c=12 |
|
| else | a,bどちらかが i で割り切れないなら 以下の処理をする |
||
| If i=2 then | |||
| i=3 | 割る数を3,5,7,…と増やす | [3] i=3 | |
| Else | |||
| i=i+2 | ※ | [5] i=5 | |
| End if | |||
| End if | |||
| Loop until ((a<i) or (b<i)) | aかｂが 割る数 i より 小さくなったら終わり |
[5] i=5 a=4,b=3 ループ終わり |
|
| print c | 最大公約数はc | c=12 | |
| print a*b*c | 最小公倍数はa*b*c | a=4､b=3 |
※ 本来ならｉは素数なのだが、簡略化するために3以降は奇数にしている。
a=48 b=36 の場合、最大公約数は12、最小公倍数は144となる。
子供のころからずっと４つの数字の合計をしてきたが、最近はボケ防止に複雑な計算をしている。
たとえば 5708なら
（０は１０として考えることにしている）
４個の数字の足し算 5+7+10+8=30
４個の数字のかけ算 5*7*10*8=2800
左右二つずつをかけ算して、その差（絶対値）を出す。
5*7-10*8→45
その値と４個の合計との最大公約数と最小公倍数。
45と30なので 15と90
最大公約数が大きな値になると何となく嬉しい。